जेव्हा ते येते तेव्हाअँटेना, लोकांना सर्वात जास्त काळजी वाटणारा प्रश्न म्हणजे "रेडिएशन प्रत्यक्षात कसे मिळवले जाते?" सिग्नल स्रोताद्वारे निर्माण होणारे इलेक्ट्रोमॅग्नेटिक फील्ड ट्रान्समिशन लाईनमधून आणि अँटेनाच्या आत कसे पसरते आणि शेवटी अँटेनापासून "वेगळे" होऊन मोकळी जागा लहरी कशी तयार होते.
१. सिंगल वायर रेडिएशन
आकृती १ मध्ये दाखवल्याप्रमाणे, qv (Coulomb/m3) म्हणून व्यक्त केलेली चार्ज घनता, a च्या क्रॉस-सेक्शनल क्षेत्रफळ आणि V च्या आकारमानासह एका वर्तुळाकार वायरमध्ये समान रीतीने वितरित केली आहे असे गृहीत धरू.
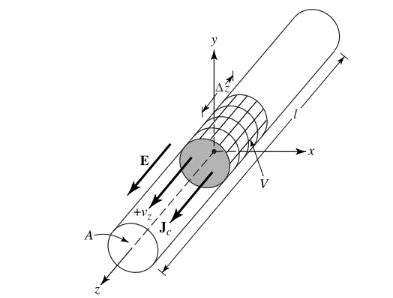
आकृती १
आकारमान V मधील एकूण चार्ज Q हा z दिशेने Vz (m/s) एका समान वेगाने फिरतो. वायरच्या क्रॉस सेक्शनवरील विद्युत् प्रवाह घनता Jz आहे हे सिद्ध करता येते:
Jz = qv vz (1)
जर तार आदर्श वाहकापासून बनलेली असेल, तर तारेच्या पृष्ठभागावरील विद्युतधारा घनता Js असेल:
जेएस = क्यूएस व्हीझेड (२)
जिथे qs ही पृष्ठभागावरील चार्ज घनता आहे. जर वायर खूप पातळ असेल (आदर्शपणे, त्रिज्या 0 असेल), तर वायरमधील विद्युतधारा खालीलप्रमाणे व्यक्त करता येते:
Iz = ql vz (3)
जिथे ql (कुलंब/मीटर) हे प्रति युनिट लांबीचे शुल्क आहे.
आपण प्रामुख्याने पातळ तारांशी संबंधित आहोत आणि वरील तीन प्रकरणांमध्ये निष्कर्ष लागू होतात. जर विद्युतधारा वेळेनुसार बदलत असेल, तर वेळेच्या संदर्भात सूत्र (3) चे व्युत्पन्न खालीलप्रमाणे आहे:
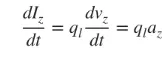
(४)
az हा चार्ज प्रवेग आहे. जर वायरची लांबी l असेल, तर (4) खालीलप्रमाणे लिहिता येईल:
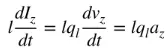
(५)
समीकरण (५) हे विद्युतधारा आणि विद्युतभार यांच्यातील मूलभूत संबंध आहे, तसेच विद्युतचुंबकीय किरणोत्सर्गाचा मूलभूत संबंध आहे. सोप्या भाषेत सांगायचे तर, किरणोत्सर्ग निर्माण करण्यासाठी, वेळेनुसार बदलणारा विद्युतधारा किंवा प्रवेग (किंवा मंदावणे) असणे आवश्यक आहे. आपण सहसा वेळेनुसार बदलणाऱ्या अनुप्रयोगांमध्ये विद्युतधारेचा उल्लेख करतो आणि चार्जचा उल्लेख बहुतेकदा क्षणिक अनुप्रयोगांमध्ये केला जातो. विद्युतभार प्रवेग (किंवा मंदावणे) निर्माण करण्यासाठी, वायर वाकलेली, दुमडलेली आणि विरहित असणे आवश्यक आहे. जेव्हा विद्युतभार वेळ-हार्मोनिक गतीमध्ये दोलन करतो, तेव्हा ते नियतकालिक विद्युतधारा (किंवा मंदावणे) किंवा वेळेनुसार बदलणारा प्रवाह देखील निर्माण करेल. म्हणून:
१) जर चार्ज हलला नाही, तर विद्युत प्रवाह आणि रेडिएशन राहणार नाही.
२) जर चार्ज स्थिर वेगाने फिरत असेल तर:
अ. जर तार सरळ आणि अनंत लांबीची असेल तर रेडिएशन होणार नाही.
b. आकृती २ मध्ये दाखवल्याप्रमाणे, जर तार वाकलेली, दुमडलेली किंवा खंडित असेल, तर रेडिएशन असते.
३) जर कालांतराने चार्ज दोलन करत राहिला, तर वायर सरळ असली तरीही चार्ज रेडिएट होईल.
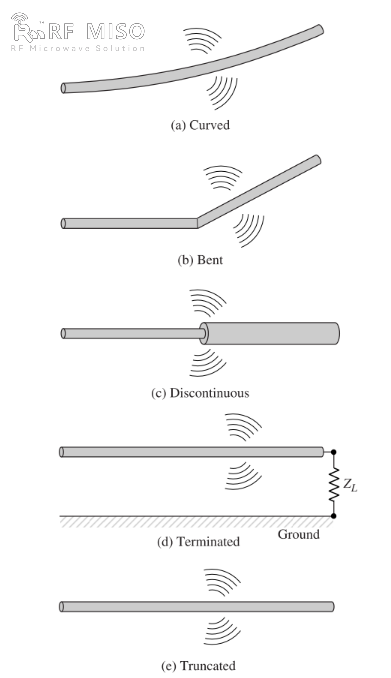
आकृती २
आकृती २(ड) मध्ये दाखवल्याप्रमाणे, उघड्या तारेशी जोडलेल्या स्पंदित स्रोताकडे पाहून रेडिएशन यंत्रणेची गुणात्मक समज मिळवता येते, जी त्याच्या उघड्या टोकावरील भाराद्वारे जमिनीवर ठेवता येते. जेव्हा तार सुरुवातीला ऊर्जावान होते, तेव्हा तारेतील चार्जेस (मुक्त इलेक्ट्रॉन) स्त्रोताद्वारे निर्माण होणाऱ्या विद्युत क्षेत्र रेषांद्वारे गतिमान होतात. वायरच्या स्रोताच्या टोकावर चार्जेस प्रवेगित होतात आणि त्याच्या टोकावर परावर्तित झाल्यावर मंदावतात (मूळ गतीच्या सापेक्ष नकारात्मक प्रवेग), त्याच्या टोकांवर आणि तारेच्या उर्वरित भागात एक रेडिएशन क्षेत्र तयार होते. चार्जेसचे प्रवेग बाह्य बलाच्या स्त्रोताद्वारे साध्य केले जाते जे चार्जेस गतिमान करते आणि संबंधित रेडिएशन क्षेत्र तयार करते. वायरच्या टोकांवर चार्जेसचे मंदावणे प्रेरित क्षेत्राशी संबंधित अंतर्गत बलांद्वारे साध्य केले जाते, जे वायरच्या टोकांवर केंद्रित शुल्कांच्या संचयनामुळे होते. वायरच्या टोकांवर चार्जेसचा वेग शून्यावर कमी झाल्यामुळे अंतर्गत बल चार्जच्या संचयनातून ऊर्जा मिळवतात. म्हणून, विद्युत क्षेत्राच्या उत्तेजनामुळे होणारे शुल्काचे प्रवेग आणि वायर प्रतिबाधाच्या विसंगती किंवा गुळगुळीत वक्रमुळे होणारे शुल्काचे मंदावणे हे इलेक्ट्रोमॅग्नेटिक रेडिएशनच्या निर्मितीसाठी यंत्रणा आहेत. जरी मॅक्सवेलच्या समीकरणांमध्ये विद्युत प्रवाह घनता (Jc) आणि शुल्क घनता (qv) दोन्ही स्त्रोत संज्ञा आहेत, तरीही चार्ज हा अधिक मूलभूत प्रमाण मानला जातो, विशेषतः क्षणिक क्षेत्रांसाठी. जरी किरणोत्सर्गाचे हे स्पष्टीकरण प्रामुख्याने क्षणिक अवस्थांसाठी वापरले जात असले तरी, ते स्थिर-स्थितीतील किरणोत्सर्गाचे स्पष्टीकरण देण्यासाठी देखील वापरले जाऊ शकते.
अनेक उत्कृष्ट शिफारस कराअँटेना उत्पादनेद्वारे उत्पादितआरएफएमआयएसओ:
२. दोन-वायर रेडिएशन
आकृती 3(a) मध्ये दाखवल्याप्रमाणे, अँटेनाशी जोडलेल्या दोन-वाहक ट्रान्समिशन लाईनला व्होल्टेज स्रोत जोडा. दोन-वायर लाईनला व्होल्टेज लावल्याने कंडक्टरमध्ये विद्युत क्षेत्र निर्माण होते. विद्युत क्षेत्र रेषा प्रत्येक कंडक्टरशी जोडलेल्या मुक्त इलेक्ट्रॉनवर (अणूंपासून सहजपणे वेगळे होणाऱ्या) कार्य करतात आणि त्यांना हालचाल करण्यास भाग पाडतात. शुल्कांच्या हालचालीमुळे विद्युत प्रवाह निर्माण होतो, ज्यामुळे चुंबकीय क्षेत्र निर्माण होते.
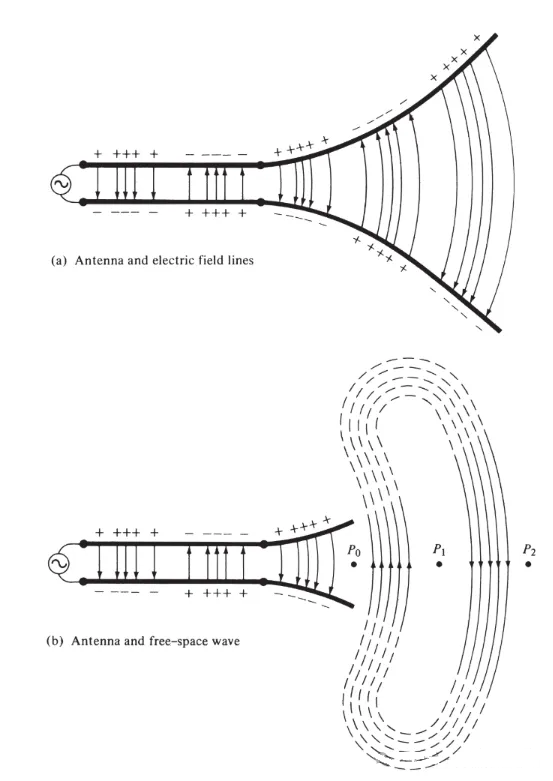
आकृती ३
आपण हे मान्य केले आहे की विद्युत क्षेत्र रेषा धन प्रभारांपासून सुरू होतात आणि ऋण प्रभारांनी संपतात. अर्थात, त्या धन प्रभारांपासून सुरू होऊन अनंतावर संपू शकतात; किंवा अनंतावर सुरू होऊन ऋण प्रभारांनी संपू शकतात; किंवा बंद लूप तयार करतात जे कोणत्याही प्रभाराने सुरू किंवा संपत नाहीत. भौतिकशास्त्रात कोणतेही चुंबकीय शुल्क नसल्यामुळे चुंबकीय क्षेत्र रेषा नेहमीच विद्युत प्रवाह वाहून नेणाऱ्या वाहकांभोवती बंद लूप तयार करतात. काही गणितीय सूत्रांमध्ये, शक्ती आणि चुंबकीय स्रोतांशी संबंधित द्रावणांमधील द्वैत दर्शविण्यासाठी समतुल्य चुंबकीय शुल्क आणि चुंबकीय प्रवाह सादर केले जातात.
दोन वाहकांमधील काढलेल्या विद्युत क्षेत्र रेषा चार्जचे वितरण दर्शविण्यास मदत करतात. जर आपण असे गृहीत धरले की व्होल्टेज स्रोत साइनसॉइडल आहे, तर आपल्याला अपेक्षा आहे की कंडक्टरमधील विद्युत क्षेत्र देखील साइनसॉइडल असेल ज्याचा कालावधी स्त्रोताच्या समान असेल. विद्युत क्षेत्राच्या ताकदीचे सापेक्ष परिमाण विद्युत क्षेत्र रेषांच्या घनतेद्वारे दर्शविले जाते आणि बाण सापेक्ष दिशा (सकारात्मक किंवा ऋण) दर्शवितात. कंडक्टरमधील वेळेनुसार बदलणाऱ्या विद्युत आणि चुंबकीय क्षेत्रांच्या निर्मितीमुळे एक इलेक्ट्रोमॅग्नेटिक वेव्ह तयार होते जी आकृती 3(a) मध्ये दर्शविल्याप्रमाणे ट्रान्समिशन लाइनवर पसरते. इलेक्ट्रोमॅग्नेटिक वेव्ह चार्ज आणि संबंधित प्रवाहासह अँटेनामध्ये प्रवेश करते. आकृती 3(b) मध्ये दर्शविल्याप्रमाणे, जर आपण अँटेना रचनेचा काही भाग काढून टाकला तर, विद्युत क्षेत्र रेषांच्या खुल्या टोकांना (बिंदू असलेल्या रेषांनी दर्शविल्याप्रमाणे) "जोडून" एक मुक्त-अवकाश लहर तयार होऊ शकते. मुक्त-अवकाश लहर देखील नियतकालिक आहे, परंतु स्थिर-चरण बिंदू P0 प्रकाशाच्या वेगाने बाहेर सरकतो आणि अर्ध्या कालावधीत λ/2 (P1 पर्यंत) अंतर प्रवास करतो. अँटेनाजवळ, स्थिरांक-चरण बिंदू P0 प्रकाशाच्या वेगापेक्षा वेगाने फिरतो आणि अँटेनापासून दूर असलेल्या बिंदूंवर प्रकाशाच्या वेगाच्या जवळ जातो. आकृती 4 मध्ये t = 0, t/8, t/4 आणि 3T/8 वर λ∕2 अँटेनाचे मुक्त-अवकाश विद्युत क्षेत्र वितरण दर्शविले आहे.
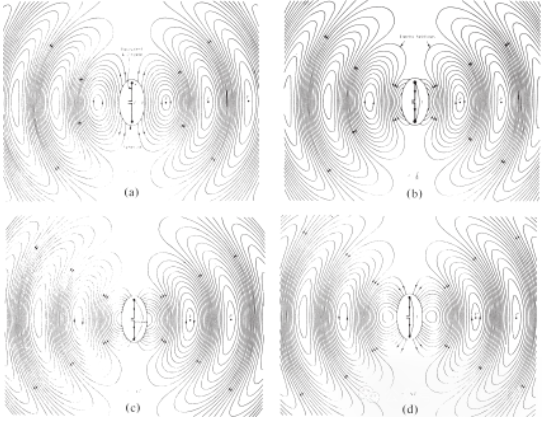
आकृती ४ t = 0, t/8, t/4 आणि 3T/8 वर λ∕2 अँटेनाचे मोकळ्या जागेचे विद्युत क्षेत्र वितरण
निर्देशित लाटा अँटेनापासून कशा वेगळ्या होतात आणि शेवटी मोकळ्या जागेत प्रसारित होण्यासाठी कशा तयार होतात हे माहित नाही. आपण निर्देशित आणि मोकळ्या जागेतील लाटांची तुलना पाण्याच्या लाटांशी करू शकतो, ज्या पाण्याच्या शांत भागात टाकलेल्या दगडामुळे किंवा इतर प्रकारे उद्भवू शकतात. एकदा पाण्यात अडथळा सुरू झाला की, पाण्याच्या लाटा निर्माण होतात आणि बाहेरून प्रसारित होऊ लागतात. जरी अडथळा थांबला तरी, लाटा थांबत नाहीत तर पुढे प्रसारित होत राहतात. जर अडथळा कायम राहिला तर, नवीन लाटा सतत निर्माण होतात आणि या लाटांचा प्रसार इतर लाटांपेक्षा मागे राहतो.
विद्युत व्यत्ययांमुळे निर्माण होणाऱ्या विद्युत चुंबकीय लाटांसाठीही हेच खरे आहे. जर स्त्रोतापासून होणारा प्रारंभिक विद्युत व्यत्यय कमी कालावधीचा असेल, तर निर्माण होणाऱ्या विद्युत चुंबकीय लाटा ट्रान्समिशन लाईनच्या आत प्रसारित होतात, नंतर अँटेनामध्ये प्रवेश करतात आणि शेवटी मुक्त अवकाश लहरी म्हणून उत्सर्जित होतात, जरी उत्तेजना आता अस्तित्वात नसली तरी (जसे पाण्याच्या लाटा आणि त्यांनी निर्माण केलेल्या व्यत्ययाप्रमाणे). जर विद्युत व्यत्यय सतत असेल, तर इलेक्ट्रोमॅग्नेटिक लाटा सतत अस्तित्वात असतात आणि प्रसारादरम्यान त्यांच्या मागे जवळून जातात, जसे आकृती 5 मध्ये दर्शविलेल्या बायकोनिकल अँटेनामध्ये दर्शविले आहे. जेव्हा इलेक्ट्रोमॅग्नेटिक लाटा ट्रान्समिशन लाईन्स आणि अँटेनाच्या आत असतात, तेव्हा त्यांचे अस्तित्व कंडक्टरच्या आत विद्युत चार्जच्या अस्तित्वाशी संबंधित असते. तथापि, जेव्हा लाटा विकिरणित होतात, तेव्हा त्या एक बंद लूप तयार करतात आणि त्यांचे अस्तित्व टिकवून ठेवण्यासाठी कोणतेही चार्ज नसते. हे आपल्याला या निष्कर्षापर्यंत पोहोचवते की:
क्षेत्राच्या उत्तेजनासाठी प्रभाराचे प्रवेग आणि मंदावणे आवश्यक असते, परंतु क्षेत्राच्या देखभालीसाठी प्रभाराचे प्रवेग आणि मंदावणे आवश्यक नसते.
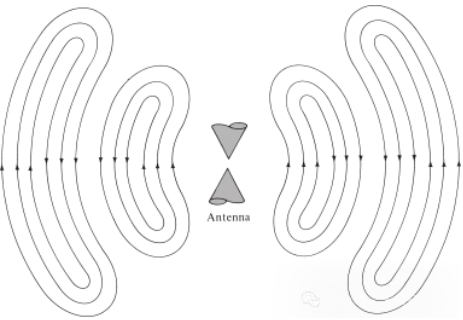
आकृती ५
३. द्विध्रुवीय विकिरण
विद्युत क्षेत्र रेषा अँटेनापासून वेगळे होऊन मुक्त-अवकाश लहरी कशा तयार करतात हे आपण स्पष्ट करण्याचा प्रयत्न करतो आणि द्विध्रुवीय अँटेनाचे उदाहरण घेतो. जरी हे एक सरलीकृत स्पष्टीकरण असले तरी, ते लोकांना मुक्त-अवकाश लहरींची निर्मिती अंतर्ज्ञानाने पाहण्यास देखील सक्षम करते. आकृती 6(a) चक्राच्या पहिल्या तिमाहीत विद्युत क्षेत्र रेषा λ∕4 ने बाहेर सरकतात तेव्हा द्विध्रुवीयच्या दोन्ही भुजांमध्ये निर्माण होणाऱ्या विद्युत क्षेत्र रेषा दर्शविते. या उदाहरणासाठी, आपण गृहीत धरू की तयार झालेल्या विद्युत क्षेत्र रेषांची संख्या 3 आहे. चक्राच्या पुढील तिमाहीत, मूळ तीन विद्युत क्षेत्र रेषा आणखी एक λ∕4 (सुरुवातीच्या बिंदूपासून एकूण λ∕2) हलवतात आणि वाहकावरील शुल्क घनता कमी होऊ लागते. हे विरुद्ध शुल्कांच्या परिचयाने तयार झाल्याचे मानले जाऊ शकते, जे चक्राच्या पहिल्या सहामाहीच्या शेवटी वाहकावरील शुल्क रद्द करतात. विरुद्ध प्रभारांमुळे निर्माण होणाऱ्या विद्युत क्षेत्र रेषा 3 आहेत आणि त्या λ∕4 चे अंतर सरकवतात, जे आकृती 6(b) मधील बिंदू असलेल्या रेषांनी दर्शविले आहे.
अंतिम परिणाम असा आहे की पहिल्या λ∕4 अंतरावर तीन खालच्या दिशेने जाणारे विद्युत क्षेत्र रेषा आहेत आणि दुसऱ्या λ∕4 अंतरावर तेवढ्याच ऊर्ध्वगामी विद्युत क्षेत्र रेषा आहेत. अँटेनावर कोणतेही निव्वळ शुल्क नसल्यामुळे, विद्युत क्षेत्र रेषा कंडक्टरपासून वेगळे होण्यास आणि एकत्र येऊन बंद लूप तयार करण्यास भाग पाडल्या पाहिजेत. हे आकृती 6(c) मध्ये दर्शविले आहे. दुसऱ्या सहामाहीत, समान भौतिक प्रक्रिया केली जाते, परंतु लक्षात ठेवा की दिशा विरुद्ध आहे. त्यानंतर, प्रक्रिया पुनरावृत्ती होते आणि अनिश्चित काळासाठी चालू राहते, आकृती 4 प्रमाणेच विद्युत क्षेत्र वितरण तयार करते.
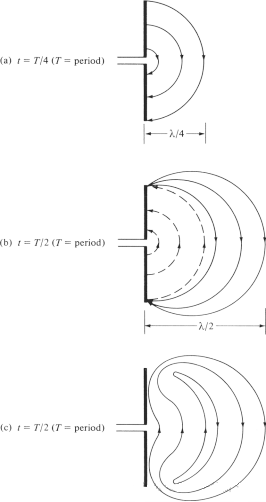
आकृती ६
अँटेनाबद्दल अधिक जाणून घेण्यासाठी, कृपया भेट द्या:
पोस्ट वेळ: जून-२०-२०२४










